【第9回】順列全探索と二分探索

競プロにおける探索

競技プログラミングにおいて探索といえば、条件を満たすような値や要素を見つけることを示すでしょう。 すべての要素から探す、すべての状況を試すといった選択を採れることは手計算には無い強みです。 第7回 で学んだ計算量の概念を意識しながら、状況に応じた効率的な探索方法を選ぶことが重要になってきます。

順列全探索

順列全探索とは、ある数列の全ての順列を列挙する方法です。順列全探索は、全ての順列を列挙するため、計算量は $O(N!)$ となります。$N$ が大きい場合は計算量が膨大になるため注意が必要で、競技プログラミングでは $N \leq 10$ 程度が限界です。

順列全探索の実装

C++ では next_permutation という関数を使うことで簡単に順列全探索を実装することができます。next_permutation は、引数に与えられた数列を次の順列に変更し、次の順列が存在する場合は true を返し、存在しない場合は false を返します。 また、ひとつ前の順列を返す prev_permutation という関数もあります。 順列全探索を行う際は、数列を昇順にソートしておくことが必要です。

以下に、数列 {1, 2, 3} の全ての順列を列挙するコードを示します。

#include <bits/stdc++.h>
using namespace std;
int main() {
    vector<int> v = {1, 2, 3};
    do {
        for (int i = 0; i < v.size(); i++) {
            cout << v.at(i) << " ";
        }
        cout << endl;
    } while (next_permutation(v.begin(), v.end()));
}

出力結果:

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

練習問題

ABC276C ABC145C ABC363C

二分探索

二分探索は、ソートされた数列に対して、探索対象の値を半分に分割して探索する方法です。二分探索は、計算量が $O(\log N)$ となるため、$N$ が大きい場合でも高速に探索することができます。
ある値が含まれているかどうかを調べるだけでなく、条件を満たす最小の値や最大の値を求めることもできます。

二分探索の実装

与えられた配列に特定の値が含まれるかを判定するプログラムの例を示します。

配列 {38, 44, 71, 57, 85, 47, 12, 91, 88, 25} に対して、値 44 が含まれているかを判定

#include <bits/stdc++.h>
using namespace std;

int main() {
    vector<int> v = {38, 44, 71, 57, 85, 47, 12, 91, 88, 25};
    sort(v.begin(), v.end()); //まずソートする
    int target = 44; //44が含まれているかを調べる
    int L = 0, R = v.size(); //Lは左端、Rは右端
    while (R - L > 1) {
        int M = (L + R) / 2; //中央のインデックス
        if (v.at(mid) <= target) { //中央の値がtarget以下なら
            L = M; //左端を中央に
        } else { //中央の値がtargetより大きいなら
            R = M; //右端を中央に
        }
    }
    if (v.at(L) == target) cout << "Found" << endl;
    else cout << "Not Found" << endl;
}

出力結果:

Found

二分探索のイメージ

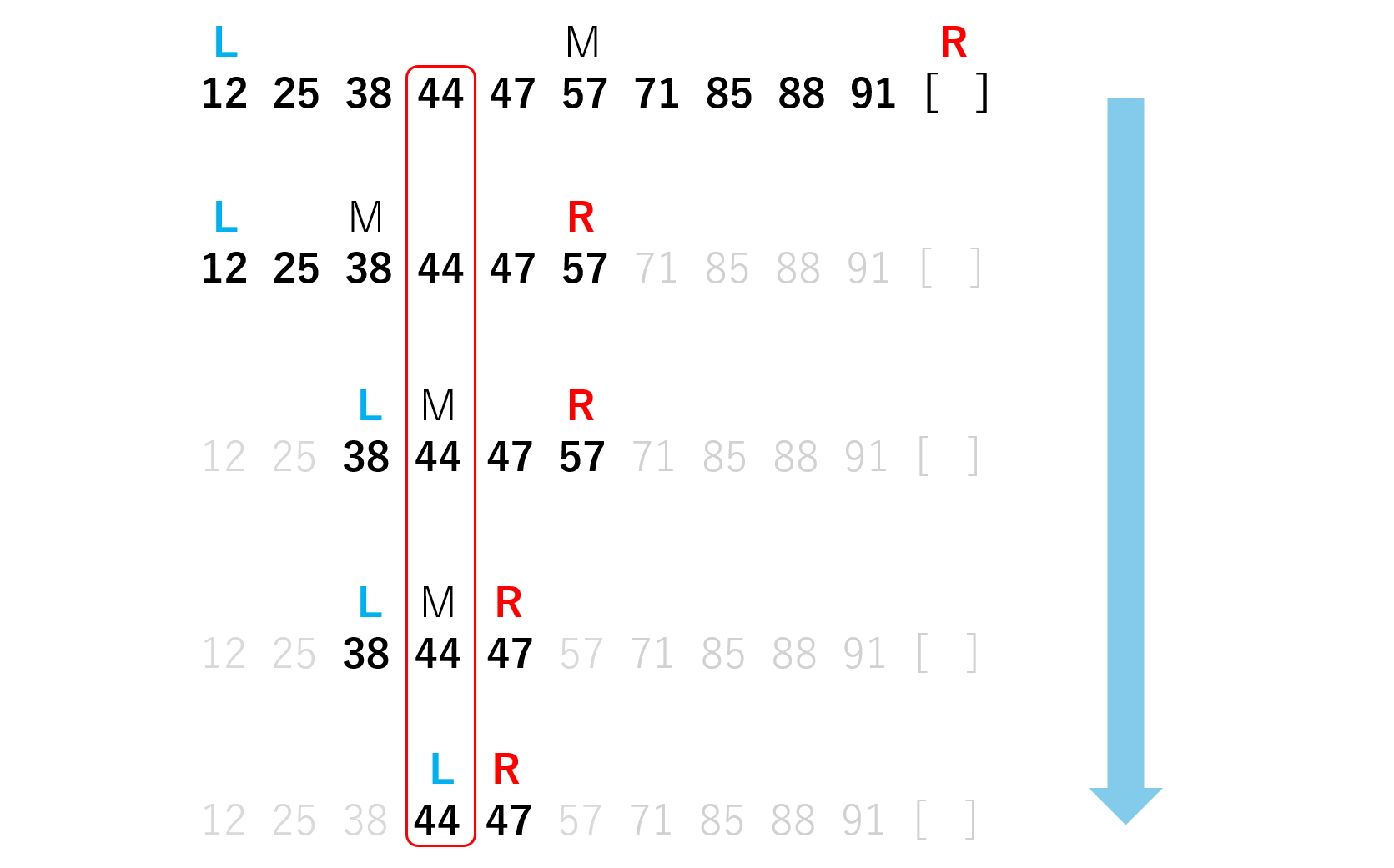
まず、配列を昇順にソートしておきます。 次に、targetの値と配列の中央の値を比較します。 中央の値がtargetの値より大きい場合、配列がソートされていることから、中央より右側に target の値があることはありません。 したがって、中央より左側の配列を探索対象とします。 同様に、中央の値がtargetの値以下の場合、左側に target の値はないので、中央より右側の配列を探索対象とします。 このようにして、探索範囲が 1 つの値となるまで探索を繰り返します。 1ステップごとに探索範囲が半分になるため、計算量は $O(\log N)$ となります。

lower_bound と upper_bound

C++ には、二分探索を行う関数として lower_bound と upper_bound と binary_search　が用意されています。 lower_bound は、指定した値以上の値が初めて現れるイテレータを返し、upper_bound は、指定した値より大きい値が初めて現れるイテレータを返します。 binary_search は、指定した値が配列に含まれているかを判定します。

練習問題

二分探索の練習問題 ABC212C ABC109B