【第14回】動的計画法(DP)　その1

動的計画法(DP)

動的計画法(DP)とは一度求めた解を利用してほかの解を求めていく解き方です。わかりやすいものとして漸化式が挙げられます。 DP法は問題の種類が多岐にわたるのですべてを説明することはできません。ですので今回は簡単なもので紹介します。

練習問題1

まず、以下の問題を解説します

この問題を解くコードは以下です

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin >> n;
    vector<int> h(n), dp(n);
    for ( int i = 0; i < n; i++ ) {
        cin >> h.at(i);
    }
    dp.at(0) = 0;
    dp.at(1) = abs(h.at(1)-h.at(0));
    for ( int i = 2; i < n; i++ ) {
        dp.at(i) = min(dp.at(i-1)+abs(h.at(i)-h.at(i-1)),dp.at(i-2)+abs(h.at(i)-h.at(i-2)));
    }
    cout << dp.at(n-1) << endl;
}

今回の問題では、それぞれの足場に移動するコストを配列 $dp$ で管理しています。
まず初期値として $dp_0=0$ , $dp_1=|h_1-h_0|$ であることは明らかです。
そして、 $i$ 番目の足場に移動する際、 $i-1$ 番目の足場か $i-2$ 番目の足場から移動する必要があるので、移動のコストとその足場までのコストの合計 $|h_i-h_{i-1}|+dp_{i-1}$ と $|h_i-h_{i-2}|+dp_{i-2}$ を比較して少ない方を $dp_i$ に代入するという方法で $i$ 番目の足場まで移動するためのコストを求めることができます。
漸化式的に書くと 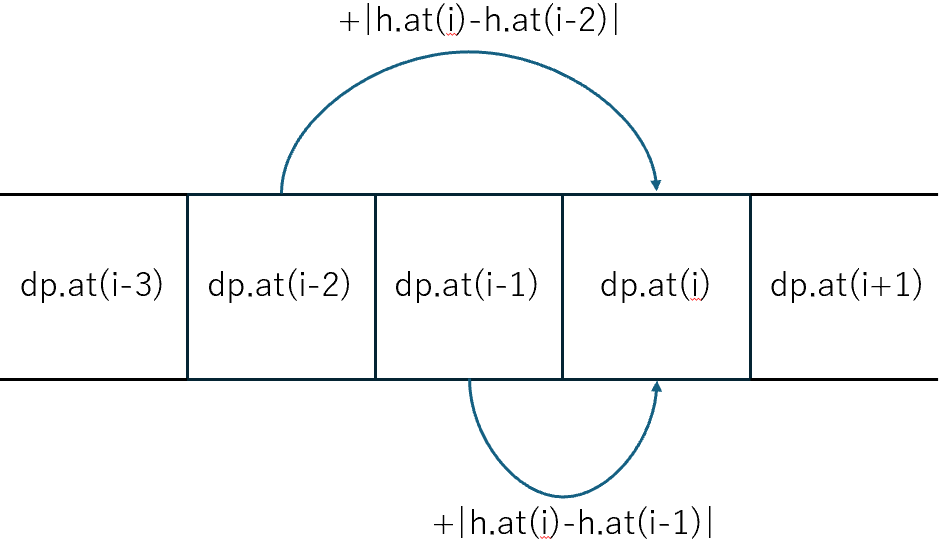$dp_i=min(|h_i-h_{i-1}|+dp_{i-1},|h_i-h_{i-2}|+dp_{i-2})$ となります。貰うDP この解き方は貰うdpと呼ばれています。
$dp_i$ が $dp_{i-1}$ や $dp_{i-2}$ から数字を貰っているためです。
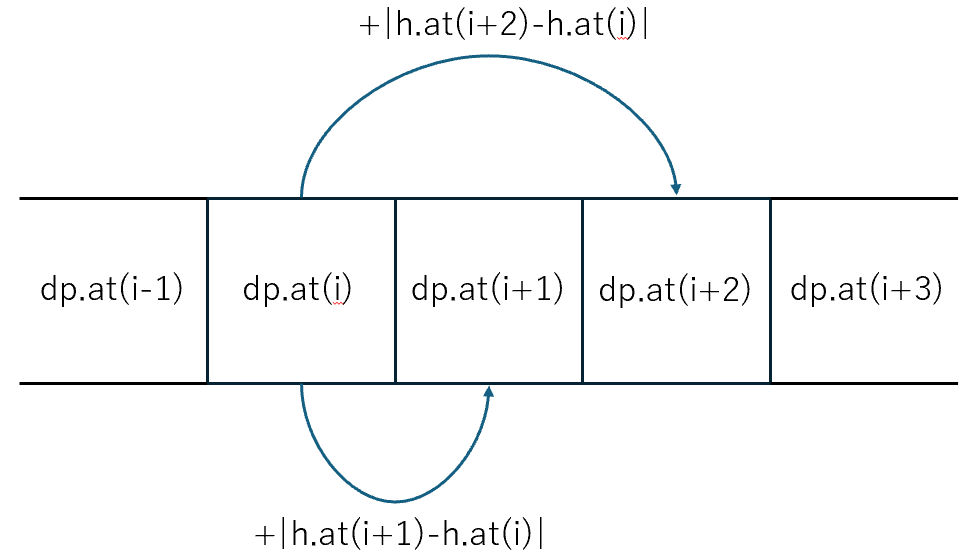
ほかには配るdpと呼ばれるものがあり、 $dp_i$ から $dp_{i+1}$ や $dp_{i+2}$ へ数値を渡す方法です。以下のように実装されます。

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin >> n;
    vector<int> h(n),dp(n,1e9);
    for ( int i = 0; i < n; i++ ) {
        cin >> h.at(i);
    }
    dp.at(0) = 0;
    for ( int i = 0; i < n-1; i++ ) {
        dp.at(i+1) = min(dp.at(i+1), dp.at(i)+abs(h.at(i+1)-h.at(i)));
        if(i+2<n){
            dp.at(i+2) = min(dp.at(i+2), dp.at(i)+abs(h.at(i+2)-h.at(i)));
        }
    }
    cout << dp.at(n-1) << endl;
}

配るDP

練習問題2

次にナップサック問題と呼ばれるものを紹介します。

$dp$ の配列を多次元にすることで考える要素が増えた場合も解くことができます。

解答例としては以下のようになります。

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n, w;
    cin >> n >> w;
    vector<long long> weight(n), value(n);
    for ( int i = 0; i < n; i++ ) {
        cin >> weight.at(i) >> value.at(i);
    }
    vector<vector<long long>> dp(n+1,vector<long long>(w+1,0));
    for ( int i = 0; i < n; i++ ) {
        for ( int j = 0; j <= w; j++ ) {
            if ( j >= weight.at(i) ) {
                dp.at(i+1).at(j) = max(dp.at(i).at(j),dp.at(i).at(j-weight.at(i))+value.at(i));
            }
            else {
                dp.at(i+1).at(j) = dp.at(i).at(j);
            }
        }
    }
    cout << dp.at(n).at(w) << endl;
}

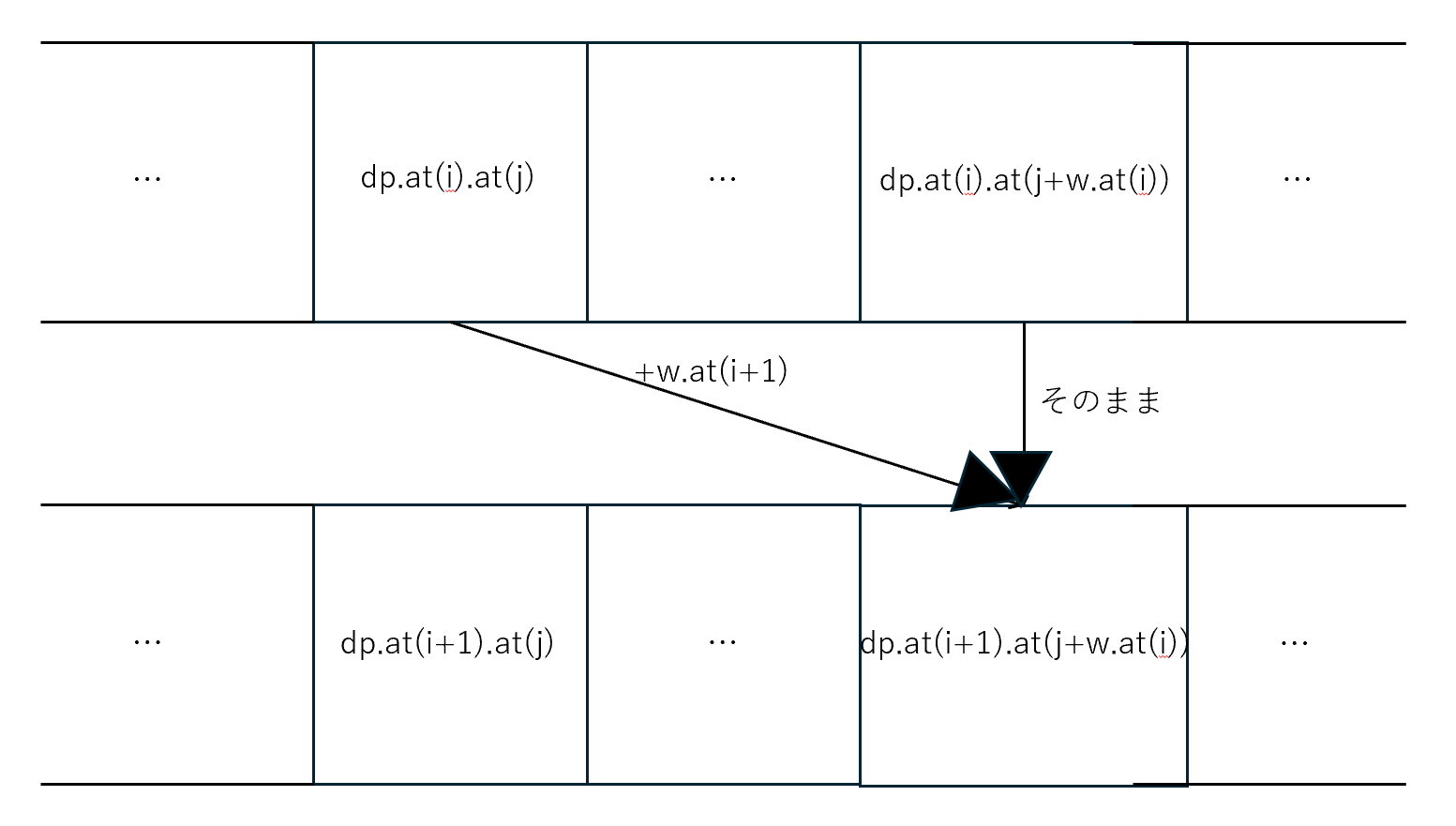
今回、配列 $dp$ を2次元配列として持っています。
$dp_{i,j}$ の $i$ は $i$ 個目までの商品を考えていることを意味し、 $j$ はナップサックの中の重みを意味します。下記のような遷移をすることで $dp_{i,j}$ の最大値を考えられます。ナップサックdp

問題集

Educational DP Contest (通称EDPC)というものがあります。後半は難しいですが序盤であれば解ける問題もあると思います。

↓今回例題で解説した問題の発展

↓その他の問題

【第14回】動的計画法(DP) その1

動的計画法(DP)

練習問題1

練習問題2

問題集

【第13回】Dijsktra法

【第14回】動的計画法(DP)　その1