累積和とは
累積和については、過去の記事を参考にしてください。
累積和で高速処理をしてみよう
いもす法
いもす法とは、累積和のアルゴリズムを多次元，多次数に拡張したものです。
引用元: https://imoz.jp/algorithms/imos_method.html
具体的には更新範囲の境界部分のみを変更し、最終的に累積和を取ることによって正しい答えを得る方法です。
例題
文章で説明するのは難しいので問題を利用して説明します。
解説
まず、すべての時間に対応した配列を作り、その時間に利用されるお湯の量を足していき、その量がを超えないかどうかを確認する、という方法が考えられます。
#include <bits/stdc++.h>
using namespace std;
int main() {
long long n, w;
cin >> n >> w;
vector<long long> s(n), t(n), p(n), check(200001);
for ( int i = 0; i < n; i++ ) {
cin >> s.at(i) >> t.at(i) >> p.at(i);
for ( int j = s.at(i); j < t.at(i); j++ ) {
check.at(j) += p.at(i);
}
}
for ( int i = 0; i < check.size(); i++ ) {
if ( check.at(i) > w ) {
cout << "No" << endl;
return 0;
}
}
cout << "Yes" << endl;
}
しかし、 は最大でであるので計算量は最大でとなり、TLEしてしまいます。
そこで、check.at(s.at(i))にp.at(i)を足し、check.at(t.at(i))からp.at(i)を引き、最終的に累積和を取ることで答えを得られます。
例えば入力が
2 6
3 5 3
1 6 2
であった場合、以下のようにします。
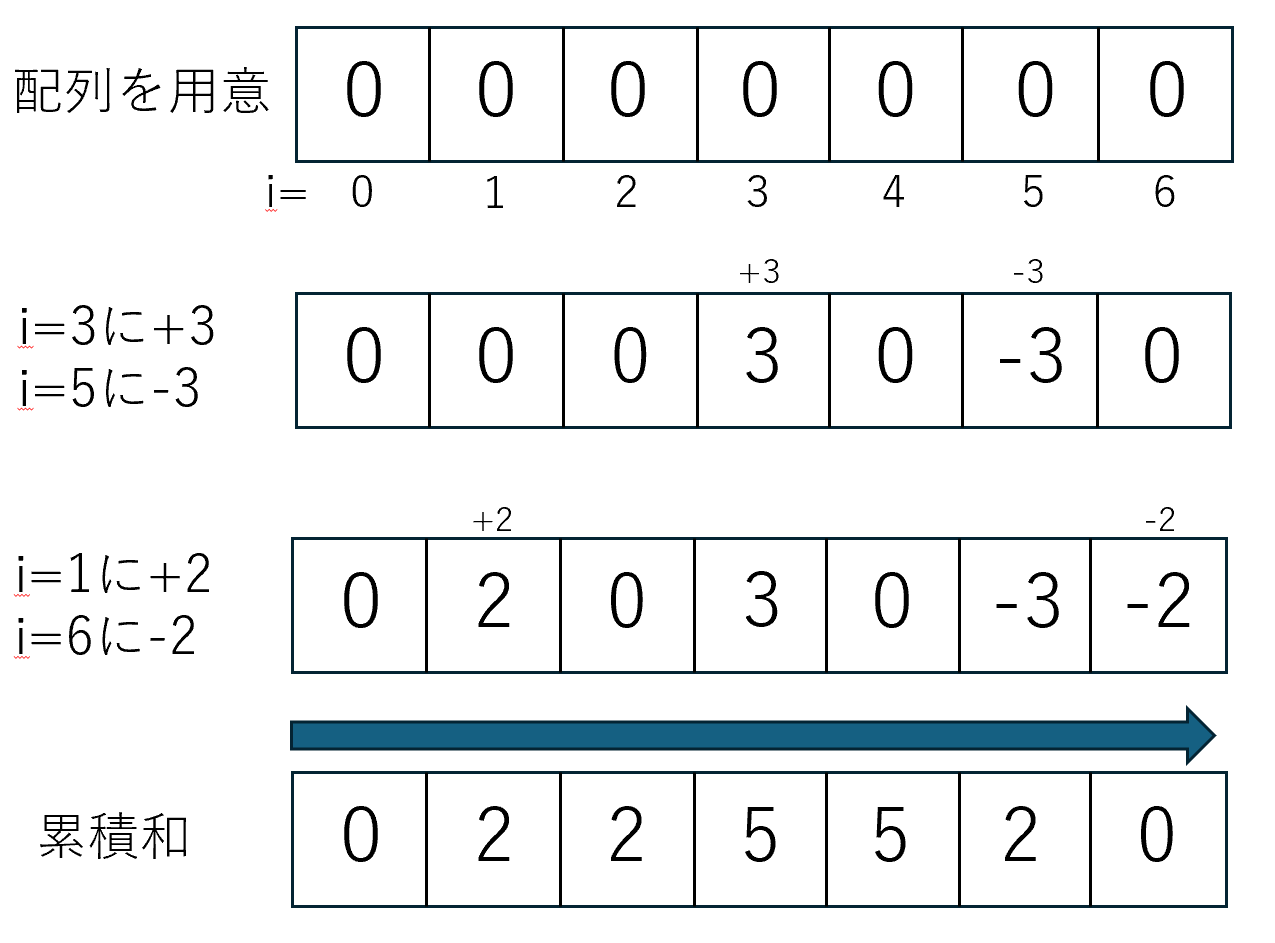この例ではを超えることがないのでYESを出力します。
最終的なコードは以下のようになります。
#include <bits/stdc++.h>
using namespace std;
int main() {
long long n, w;
cin >> n >> w;
vector<long long> s(n), t(n), p(n), check(200001);
for ( int i = 0; i < n; i++ ) {
cin >> s.at(i) >> t.at(i) >> p.at(i);
check.at(s.at(i)) += p.at(i);
check.at(t.at(i)) -= p.at(i);
}
for ( int i = 1; i < check.size(); i++ ) {
check.at(i) += check.at(i-1);
}
for ( int i = 0; i < check.size(); i++ ) {
if ( check.at(i) > w ) {
cout << "No" << endl;
return 0;
}
}
cout << "Yes" << endl;
}
これの書き方であれば計算量は多くともであり、間に合います。
この解き方がいもす法と呼ばれています。
また、いもす法は１次元でなくとも利用することができます。
練習問題
最後の問題は２次元いもす法を使います。