【第7回】全探索と二分探索

入門講習会第7回

Homeブログ一覧【第7回】全探索と二分探索

全探索とは

全探索とは、その名の通り、全てのパターンを試すことです。以下のような例題を考えましょう。

1 から 100 までの整数のうち、好きな数を 3 つ選んで足し合わせると、ちょうど 100 になる自然数の組 (i,j,k)(i,j,k) は何通りあるでしょうか？3 つの数字は重複しても構いません。

これは 3 重ループで全てのパターンを試せば解くことができます。計算量は N=100N=100 として O(N3)O(N^3) となります。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int cnt = 0;
    for(int i = 1; i <= 100; i++){
        for(int j = 1; j <= 100; j++){
            for(int k = 1; k <= 100; k++){
                if(i + j + k == 100) cnt++;
            }
        }
    }
    cout << cnt << endl;
}

これは計算量を落として、 O(N2)O(N^2) にすることができます。 ii と jj を決めた時に、 kk は 100−i−j100 - i - j で決まるからです。この計算量を落とすテクニックは、全探索で使うことがあるので覚えておきましょう。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int cnt = 0;
    for(int i = 1; i <= 100; i++){
        for(int j = 1; j <= 100; j++){
            int k = 100 - i - j;
            if(k >= 1 && k <= 100) cnt++;
        }
    }
    cout << cnt << endl;
}

二分探索とは

二分探索とは、ソートされた配列に対して、ある値が含まれているかどうかを O(log⁡N)O(\log N) で判定するアルゴリズムです。以下のような例題を考えましょう。

昇順に並べられた配列 [12,34,56,63,76,89,90] に対して、値 89 が含まれているかどうかを判定してください。

二分探索では、探索範囲を [L,R)[L, R) として、中央の番号 M=⌊L+R2⌋M = \lfloor \dfrac{L + R}{2} \rfloor に注目します。 配列はソートされていることに注意すると、 aMa_M が探索したい値より大きい場合、次の探索範囲は [L,M)[L, M) になり、探索したい値以下の場合は [M,R)[M, R) となります。 この操作を、 [L,R)[L, R) の要素数が 1 となる、すなわち R−L=1R - L = 1 となるまで繰り返します。

#include <bits/stdc++.h>
using namespace std;

int main(){
    vector<int> a = {12,34,56,63,76,89,90};
    int x = 89;
    int L = 0, R = a.size();
    while(R - L > 1){
        int M = (L + R) / 2;
        if(a[M] > x) R = M;
        else L = M;
    }
    if(a[L] == x) cout << "found" << endl;
    else cout << "not found" << endl;
}

上の問題では、まず探索範囲を [0,7)[0, 7) とします。 image

L=0,R=7L = 0, R = 7 なので、 M=3M = 3 とします。 a3=63a_3 = 63 は 8989 以下なので、89 はこれの右側にあるはずです。 よって、次の探索範囲は [3,7)[3, 7) となり、 M=5M = 5 になります。

image

a5=89a_5 = 89 は 8989 以下なので、(便宜上) 89 は右側にあります。 よって、次の探索範囲は [5,7)[5, 7) となり、 M=6M = 6 です。

image

a6=90a_6 = 90 ですが、89 より大きいので、次の探索範囲は [5,6)[5, 6) になります。

image

この区間に含まれる番号は 55 のみなので、ループを抜け、 a5=89a_5 = 89 かどうかの判定をすればよいです。

c++には二分探索を行う関数が用意されています。

関数名説明
lower_bound探索したい値以上の最初の要素のイテレータ
upper_bound探索したい値より大きい値の最初のイテレータ

どちらも、探索したい値が見つからなかった場合は、配列の末尾(変数名.end())を指します。

イテレータってなに？

イテレータは、コンテナの要素を参照、移動、変更などができる便利なものです。イテレータを使うことで、配列の要素を簡単に操作することができます。sort,max_element,min_elementなどで使うbegin(),end()もイテレータです。イテレータは半開区間のようなイメージを持っておくと分かりやすいかもしれません。

image

#include <bits/stdc++.h>
using namespace std;

int main(){
    vector<int> a = {12,34,56,63,76,89,90};
    int x = 89;
    auto itr=lower_bound(a.begin(),a.end(),x);
    // *itrでイテレータの指す値を取得できる。今回は89になる。
    if(itr != a.end() && *itr == x) cout << "found" << endl;
    else cout << "not found" << endl;
}

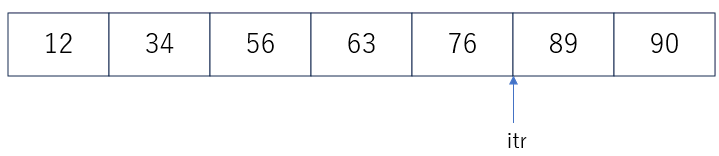
image

set にも同様の関数が用意されています。setの場合は、a.lower_bound(x)のように使います。 lower_bount(a.begin(),a.end(),x)のようにもできますが、ランダムアクセスイテレータではないので遅いです。 詳しくはこのコードにいい感じのことが書いてあります。https://qiita.com/yaskitie/items/da225f5ab13bb6d3221e

#include <bits/stdc++.h>
using namespace std;

int main(){
    set<int> a = {12,34,56,63,76,89,90};
    int x = 89;
    auto itr=a.lower_bound(x);
    if(itr != a.end() && *itr == x) cout << "found" << endl;
    else cout << "not found" << endl;
}

おまけ　三分探索

二分探索のほかに、三分探索があります。三分探索は関数の極大、極小を求めるときに使います。今回はあまり深くは話さないので、興味がある人は調べてみてください。 https://qiita.com/ganyariya/items/1553ff2bf8d6d7789127

練習問題

全探索の問題

問題 1:ABC087 B

ヒント

三重ループで全探索してみましょう。

解答例
#include <bits/stdc++.h>
using namespace std;

int main() {
    int a, b, c, x;
    cin >> a >> b >> c >> x;
    int ans = 0;
    for (int i = 0; i <= a; i++) {
        for (int j = 0; j <= b; j++) {
            for (int k = 0; k <= c; k++) {
                if (500 * i + 100 * j + 50 * k == x) ans++;
            }
        }
    }
    cout << ans << endl;
    return 0;
}

問題 2:ABC072 C

ヒント

a[i]a[i] を操作してなりうる値の個数を数えよう。

解答例
#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++) cin >> a[i];

    int ans = 0;
    vector<int> cnt(100000);
    for (int i = 0; i < n; i++) {
        cnt[a[i]]++;
        if (a[i] - 1 >= 0) cnt[a[i] - 1]++;
        if (a[i] + 1 < 100000) cnt[a[i] + 1]++;
    }
    for (int i = 0; i < 100000; i++) {
        ans = max(ans, cnt[i]);
    }
    cout << ans << endl;
}

二分探索の問題

問題 3:ABC212 C

ヒント

二分探索を使って、 a[i]a[i] に最も近い値を配列 bb から探そう。

解答例
#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n), b(m);
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < m; i++) cin >> b[i];
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());

    // 二分探索する
    int ans = 1e9;
    for (int i = 0; i < n; i++) {
        auto itr = lower_bound(b.begin(), b.end(), a[i]);
        if (itr != b.end()) ans = min(ans, abs(a[i] - *itr));
        if (itr != b.begin()) ans = min(ans, abs(a[i] - *(itr - 1)));
    }
    cout << ans << endl;
}

問題 5:ARC109 B

ヒント

長さ n+1n+1 の丸太を買って、短い丸太を作れるだけ作った後に、残りの丸太を買うのが最適です。 n+1n+1 の長さの丸太をいくつの丸太に切ればいいかを二分探索で求めましょう。具体的には、 1+⋯+k≤n+11+ \dots +k \leq n+1 を満たす最大の kk を求めます。

解答例
#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
    ll n;
    cin >> n;
    ll l = 0, r = 2e9;  // 2e9 = 2 * 10^9
    while (r - l > 1) {
        ll mid = (l + r) / 2;
        if (mid * (mid + 1) / 2 <= n + 1) l = mid;
        else r = mid;
    }
    cout << n - l + 1 << endl;
}

【第6回】累積和で高速処理をしてみよう

【第8回】確率DPと期待値DP